Have you ever found yourself looking at a nine-sided shape, perhaps a badge or a unique piece of art, and wondered about its angles or how much space it covers? Nonagons, these interesting geometric figures, often pop up in unexpected places, and figuring out their properties can be a bit of a brain-teaser for many people. It's almost like trying to solve a puzzle without all the right pieces, you know?
For students tackling geometry homework or anyone curious about the math behind everyday shapes, a nonagon can seem pretty complex. You might be asked to find a missing angle, figure out the total perimeter, or even determine its area. These tasks can get pretty tricky, especially when you are dealing with many different numbers and formulas, so it can be quite a challenge.
That is where a good nonagon calculator truly shines, providing a helpful hand. This simple tool takes away the fuss of manual calculations, letting you quickly find answers to all sorts of questions about these nine-sided forms. It makes working with nonagons much more straightforward, actually, which is pretty neat.
Table of Contents
- What is a Nonagon, Anyway?
- Why a Nonagon Calculator is a Great Tool
- How to Use a Nonagon Calculator
- Common Questions About Nonagons
- The Future of Geometry Tools
- Making Math Simple with a Nonagon Calculator
What is a Nonagon, Anyway?
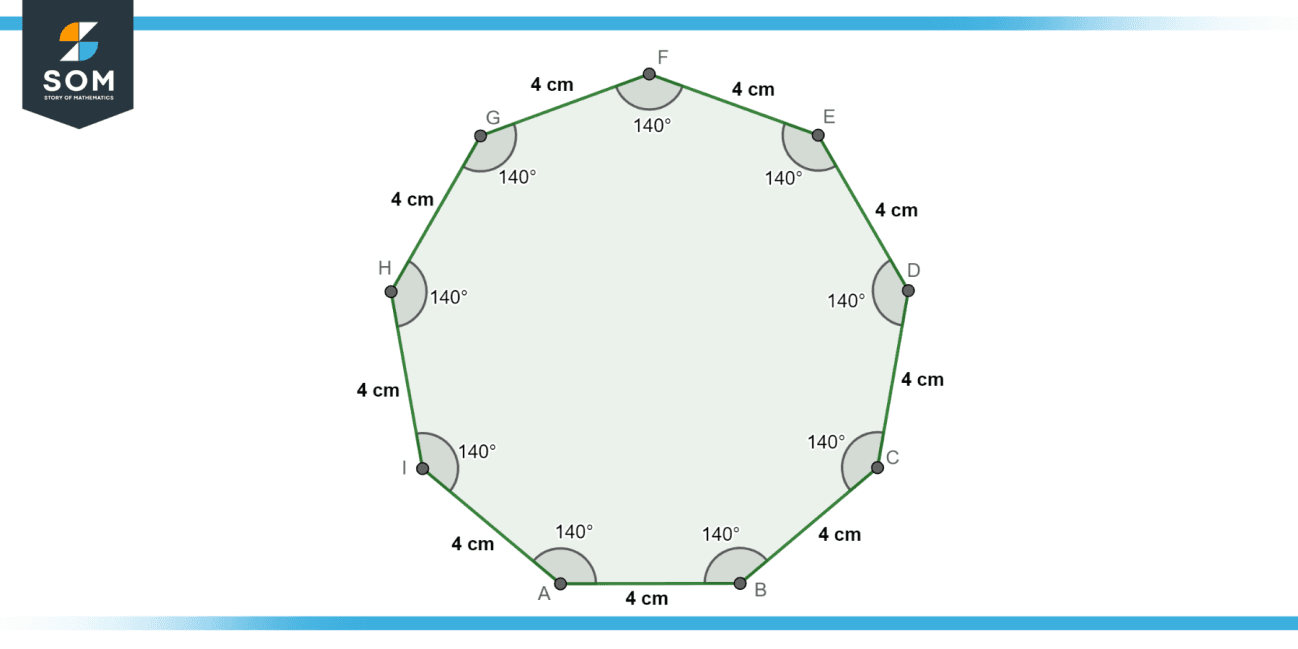
A nonagon is a polygon, which is a flat shape with straight sides, that has nine sides and nine angles. The word "nona" means nine, so it makes perfect sense, doesn't it? These shapes can be regular, meaning all their sides are the same length and all their angles are the same size, or they can be irregular, with sides and angles that vary.
Regular nonagons, in particular, have a very balanced look to them. You might spot them in architectural designs, certain logos, or even in some board games. Understanding their properties, like the sum of their interior angles, is a basic part of geometry, so that is pretty important.
The total measure of the interior angles in any nonagon, regular or irregular, always adds up to a specific number. This is a fixed rule in geometry. Knowing this sum is often the first step in figuring out unknown angles within the shape, which is quite useful for solving problems, like the ones you might find in a textbook, you know.
Why a Nonagon Calculator is a Great Tool
A nonagon calculator really simplifies things when you are dealing with these shapes. It takes away the need for long, manual calculations that can sometimes lead to errors. This tool is, in a way, a handy assistant for anyone working with nonagons, making the process much smoother and faster.
Think about it: instead of remembering complex formulas or doing a lot of arithmetic by hand, you just input the numbers you have. The calculator then does the heavy lifting for you. This means you get accurate results quickly, which is a real time-saver, especially if you are on a deadline, or just want to check your work, basically.
It helps you avoid simple mistakes, too. Even experienced people can make small errors when calculating by hand. A calculator removes that risk, giving you reliable answers every time. This reliability is a big part of why these tools are so popular and useful, as a matter of fact.
Solving for Missing Angles
One common problem involves finding an angle when you know the others. For example, if you have a nonagon where seven of the angles are 138°, 154°, 145°, 132°, 128°, 147°, and 130°, and the two remaining angles are equal, finding those last two can be a bit of a puzzle. A nonagon calculator can help with this, very quickly.
You see, the sum of all interior angles in a nonagon is always 1260 degrees. If you add up the seven known angles, you get 974 degrees. Then, you subtract that from 1260 degrees, leaving 286 degrees for the two equal angles. Dividing 286 by two gives you 143 degrees for each of the missing angles, so that is how it works out.
A calculator can do these steps for you, or at least help you verify your own calculations very fast. You might input the known angles, and it could tell you the sum. Then, you just do a couple of simple subtractions and divisions to find the unknowns. It makes a complex problem quite manageable, you know, which is helpful.
Finding the Perimeter
The perimeter of any polygon is just the total length of all its sides added together. For a nonagon, that means summing up nine different lengths. If you have an irregular nonagon with sides measuring, say, 8, 13, 11, 21, 10, 7, 9, 10, and 3 units, adding them all up by hand can take some time.
A nonagon calculator, or even a basic sum function, makes this quick and simple. You just punch in each side length, and it gives you the total. For the example numbers, the sum is 92 units, which is pretty straightforward. This is especially useful for shapes with many sides, where manual addition can get tedious, basically.
If you are working with a regular nonagon, finding the perimeter is even easier. You just need the length of one side, and then you multiply that by nine. A calculator helps you do this multiplication without any fuss, giving you the answer right away. It is a simple task, but the calculator makes it even more efficient, actually.
Calculating the Area
Finding the area of a nonagon, especially a regular one, usually involves a specific formula that uses its apothem and side length. The apothem is the distance from the center of the polygon to the midpoint of any side. This can be a bit more involved than just adding up sides, you know.
For instance, imagine you have a regular nonagon with an apothem of 5.6 cm and a side length of 4.1 cm. The formula for the area of a regular polygon is (1/2) * apothem * perimeter. First, you would find the perimeter: 9 sides * 4.1 cm/side = 36.9 cm. Then, (1/2) * 5.6 cm * 36.9 cm = 103.32 cm². A calculator is really good for these kinds of calculations, very quickly.
Another example: a regular nonagon with an apothem of 50.9 cm and a side length of 37 cm. The perimeter would be 9 * 37 cm = 333 cm. Then, (1/2) * 50.9 cm * 333 cm = 8474.85 cm². Doing these multiplications and divisions by hand can be quite a chore, so a calculator truly comes in handy for these types of problems, obviously.
A nonagon calculator can often take these values directly and give you the area. Some advanced calculators might even have a dedicated function for polygon areas. This saves you from having to remember the formula or perform multi-step arithmetic yourself. It is a big help for accuracy, too, which is important.
Understanding Rotational Symmetry
Regular nonagons have a special kind of symmetry called rotational symmetry. This means you can rotate the shape around its center, and it will look exactly the same before it completes a full circle. For a regular nonagon, there are nine such rotational symmetries.
The angle of rotation for each of these symmetric positions is found by dividing 360 degrees by the number of sides, which is nine. So, 360 / 9 equals 40 degrees. This means if you rotate a regular nonagon by 40 degrees, or any multiple of 40 degrees, it will perfectly align with its original position.
If you are asked to find the angle of rotation that maps one vertex to another, say from 'd' to 'i' on a regular nonagon, a calculator can help you figure out the multiples of 40 degrees. You count how many "jumps" it takes from 'd' to 'i' around the center. Each jump is 40 degrees, so you multiply that by the number of jumps. This is a pretty straightforward use of the calculator, actually.
Interior and Exterior Angles
Every regular nonagon has interior angles that are all the same measure. We know the sum of all interior angles is 1260 degrees. Since there are nine angles, you just divide 1260 by 9. This gives you 140 degrees for each interior angle of a regular nonagon, which is a key property.
The exterior angle of any regular polygon is found by dividing 360 degrees by the number of sides. For a nonagon, that is 360 / 9, which equals 40 degrees. An interior angle and its corresponding exterior angle always add up to 180 degrees. So, 140 + 40 equals 180, which checks out, you know.
A nonagon calculator can quickly give you these angle measures. You just tell it you are looking at a regular nonagon, and it can provide the interior and exterior angle values right away. This is super helpful for checking your understanding or for quick reference, so it is a very useful feature.
How to Use a Nonagon Calculator
Using a nonagon calculator is generally very simple. Most online versions will have clear input fields where you can enter the information you have. For example, if you want to find the area, you might enter the apothem and side length. If you are looking for angles, you might input the known angle measures.
The key is to know what information you have available and what you are trying to find. The calculator then does the rest. It is a bit like filling out a form, you know, where you provide the details and it processes them. Always make sure to double-check your inputs to avoid errors in the output, which is just good practice.
Many calculators also provide a visual representation of the nonagon, which can be really helpful for understanding the properties. This visual aid can make abstract numbers feel more concrete. It is a great way to learn and verify your answers, too, which is pretty cool.
Common Questions About Nonagons
People often have similar questions when it comes to nonagons and their properties. Here are a few common ones, along with how a calculator can help:
What is the sum of the interior angles of a nonagon?
The sum of the interior angles of any nonagon, regular or irregular, is always 1260 degrees. You can get this by using the formula (n-2) * 180, where 'n' is the number of sides. For a nonagon, n=9, so (9-2) * 180 = 7 * 180 = 1260 degrees. A nonagon calculator can often show you this sum directly or help you do the multiplication, which is pretty handy.
How do you find the measure of each interior angle of a regular nonagon?
For a regular nonagon, where all angles are equal, you divide the total sum of interior angles (1260 degrees) by the number of sides (9). So, 1260 / 9 = 140 degrees. Each interior angle of a regular nonagon is 140 degrees. A nonagon calculator can give you this value instantly, which is very helpful for quick checks.
What is the angle of rotation for a regular nonagon?
The angle of rotation for a regular nonagon's rotational symmetry is 360 degrees divided by the number of sides, which is 9. So, 360 / 9 = 40 degrees. This means you can rotate it by 40 degrees, or multiples of 40 degrees, and it will look the same. A calculator makes this division simple, and you can then use it to figure out rotations between specific points, you know.
The Future of Geometry Tools
As technology keeps moving forward, online geometry tools, including the nonagon calculator, will probably become even more sophisticated. We might see more interactive features, better visual aids, and perhaps even step-by-step solutions to problems. This would make learning about shapes even more engaging and accessible for everyone.
These tools are always getting better at helping people understand complex ideas without getting bogged down in tedious math. They allow us to focus on the concepts rather than just the arithmetic. It is a very exciting time for educational resources, so that is something to look forward to.
The goal is always to make learning easier and more fun. A good nonagon calculator is just one example of how digital tools are helping us achieve that. It is pretty cool to see how far these resources have come, and where they might go next, you know.
Making Math Simple with a Nonagon Calculator
Whether you are a student trying to finish your homework, a designer working on a project, or just someone who enjoys geometry, a nonagon calculator can be a truly valuable resource. It takes the guesswork out of complex calculations and gives you accurate answers very fast. It is a simple tool, but its impact can be quite big.
This kind of calculator helps you explore the properties of nonagons without getting stuck on the numbers. It frees you up to think about the shapes themselves and how they fit into the world around us. It is, in a way, a little helper that lets you focus on the bigger picture, you know.
So, the next time you encounter a nonagon problem, remember that a handy tool is available to make your life easier. You can learn more about nonagons and their properties, and see how a calculator can assist. You can also find other geometry tools on our site, which is pretty useful.
Using a nonagon calculator means less time spent on calculations and more time spent understanding and applying geometric concepts. It is a smart way to approach math problems in today's world, which is pretty neat. It truly helps to make complex shapes approachable for everyone, which is a great thing, really.


Detail Author:
- Name : Nella Swift
- Username : justyn23
- Email : ransom.pfeffer@gmail.com
- Birthdate : 1990-07-28
- Address : 9987 Louie Forges Suite 829 Port Adrianaborough, NJ 55142
- Phone : 442.586.4125
- Company : Reichert-Koepp
- Job : Usher
- Bio : Illo temporibus exercitationem porro sed ut aspernatur porro saepe. Error nobis sunt dignissimos ipsam aut nesciunt maxime.
Socials
linkedin:
- url : https://linkedin.com/in/kabbott
- username : kabbott
- bio : Natus culpa eum quos quis id.
- followers : 3505
- following : 1005
instagram:
- url : https://instagram.com/kamren_real
- username : kamren_real
- bio : Provident corporis totam dolorum veniam laboriosam cupiditate. Iusto impedit est quas.
- followers : 2492
- following : 618
facebook:
- url : https://facebook.com/kamren_id
- username : kamren_id
- bio : Voluptate ipsam dolor et modi rerum assumenda autem.
- followers : 5483
- following : 1296
twitter:
- url : https://twitter.com/kamren_abbott
- username : kamren_abbott
- bio : Molestias et culpa laboriosam aliquam dolores mollitia. Explicabo aspernatur sapiente expedita id nesciunt porro aut est. Aspernatur molestias eaque sit ut.
- followers : 3922
- following : 995